Variabel Acak Diskrit dan Kontinue

-
VARIABEL ACAK

       Variabel acak adalah suatu fungsi yang nilainya berupa bilangan nyata yang ditentukan oleh setiap unsur dalam ruang contoh disebut peubah acak (Walpole, 1993).

          Variabel acak diskrit adalah suatu variabel acak yang memiliki nilai dicacah, sementara variabel acak kontinu memiliki nilai yang tak terhingga banyaknya sepanjang interval yang tidak terputus variabel acak kontinu diperoleh dari hasil pengukuran (Harinaldi, 2005).

Pembagian Distribusi Variabel Acak Diskrit

       Distribusi variabel acak diskrit terbagi atas distribusi seragam, distribusi binomial, distribusi multinominal, distribusi hipergeometrik, distribusi binomial negatif, distribusi geometrik dan distribusi poisson.

Penjelasan dari setiap distribusi tersebut akan dijelaskan sebagai berikut :
  1.  Distribusi Seragam

           Distribusi seragam diskrit adalah bila peubah acak x mempunyai nilai X1, X2, ... , Xk, dengan peluang yang sama, maka distribusi seragam diskritnya diberikan olehanya. (Walpole, 1993)
                                         
                                             f(x,k) = 1/k, untuk X = X1, X2, ... , Xk.... (1)

       Distribusi seragam telah menggunakan notasi f(x,k) alih-alih f(x) untuk menunjukkan bahwa seragam itu bergantung pada parameter k (Walpole, 1993).

Contoh: 
Bila sebuah dadu setimbang dilemparkan, setiap unsur ruang

         S = {1, 2, 3, 4, 5, 6} mempunyai peluang yang sama untuk muncul, yaitu 1/6. Oleh karena itu kita mempunyai Distribusiseragam dengan f(x;6) = 1/6 untuk x = 1, 2, 3, 4, 5, 6.
      
     2. Distribusi Binomial

        Distribusi binomial adalah bila suatu ulangan binomial yang mempunyai peluang keberhasilan P dan peluang kegagalan q = 1 –p, maka distribusi peluang bagi peubah acak binomial x, yaitu banyaknya keberhasilan dalam n ulangan yang bebas adalah (Walpole, 1993).

   Umumnya suatu eksperimen atau percobaan dapat dikatakan eksperimen binomial apabila memenuhi syarat berikut ini (Supranto, 2001) :
  • Banyaknya eksperimen merupakan bilangan tetap (fixed number oftrials).
  • Eksperimen mempunyai 2 hasilyang dikategorikan menjadi sukses dangagal.
  • Probabilitas sukses sama pada setiap percobaan.
  • Eksperimen tersebut harus bebassatu sama lainnya, artinya hasileksperimen yang satu tidak mempengaruhi hasil eksperimen lainnya.

       Apabila suatu himpunan yang terdiri dari n elemen dibagi dua, yaitu x sukses dan (n–x) gagal, maka banyaknya permutasi dari n elemen yang diambil x setiap kali dapat dihitung berdasarkan rumus berikut (Supranto, 2001).

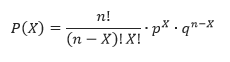
Komentar

Posting Komentar

Postingan populer dari blog ini

PROBABILITAS STATISTIKA & TEOREMA BAYES

-
Gambar
PROBABILITAS PENGERTIAN PROBABILITAS         Probabilitas atau Peluang adalah suatu ukuran tentang kemungkinan suatu peristiwa (event) akan terjadi di masa mendatang. Probabilitas dapat juga diartikan sebagai harga angka yang menunjukkan seberapa besar kemungkinan suatu peristiwa terjadi, di antara keseluruhan peristiwa yang mungkin terjadi. Probabilitas dilambangkan dengan P. Ada tiga hal penting dalam probabilitas, yaitu: Percobaan adalah pengamatan terhadap beberapa aktivitas atau proses yang memungkinkan timbulnya paling sedikit 2 peristiwa tanpa memperhatikan peristiwa mana yang akan terjadi. Hasil adalah suatu hasil dari sebuah percobaan. Peristiwa adalah kumpulan dari satu atau lebih hasil yang terjadi pada sebuah percobaan atau kegiatan. MANFAAT PROBABILITAS         Manfaat probabilitas dalam kehidupan sehari-hari adalah membantu kita dalam mengambil suatu keputusan, serta meram...
Baca selengkapnya

MACAM-MACAM DISTRIBUSI DALAM STATISTIK

-
Gambar
DISTIRBUSI BINOMINAL     Distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam npercobaan ya/tidak (berhasil/gagal) yang saling bebas, dimana setiap hasil percobaan memiliki probabilitas p. Eksperimen berhasil/gagal juga disebut  percobaan bernoulli . Ketika n = 1, distribusi binomial adalah  distribusi bernoulli . Distribusi binomial merupakan dasar dari  uji binomial  dalam uji signifikansi statistik.       Syarat Ditribusi Binominal: Setiap usaha hanya mempunyai 2 kemungkinan yaitu “sukses atau gagal”; Peluang sukses, dinyatakan dengan p, tidak berubah dari usaha yang satu ke yang berikutnya; Pengambilan sampel dilakukan dengan pengembalian ( sampling with replacement ); Percobaan terdiri atas n usaha yang berulang.      Rumus Binominal:        Dalam suatu percobaan binomial, peluang untuk mendapatkan tepat ...
Baca selengkapnya