PROBABILITAS STATISTIKA & TEOREMA BAYES
PROBABILITAS
PENGERTIAN PROBABILITAS
Probabilitas atau
Peluang adalah suatu ukuran tentang kemungkinan suatu peristiwa (event) akan
terjadi di masa mendatang. Probabilitas dapat juga diartikan sebagai harga
angka yang menunjukkan seberapa besar kemungkinan suatu peristiwa
terjadi, di antara keseluruhan peristiwa yang mungkin
terjadi. Probabilitas dilambangkan dengan P.
Ada tiga hal penting dalam probabilitas,
yaitu:
- Percobaan adalah pengamatan terhadap beberapa aktivitas atau proses yang memungkinkan timbulnya paling sedikit 2 peristiwa tanpa memperhatikan peristiwa mana yang akan terjadi.
- Hasil adalah suatu hasil dari sebuah percobaan.
- Peristiwa adalah kumpulan dari satu atau lebih hasil yang terjadi pada sebuah percobaan atau kegiatan.
Manfaat
probabilitas dalam kehidupan sehari-hari adalah membantu kita dalam mengambil
suatu keputusan, serta meramalkan kejadian yang mungkin terjadi. Jika kita
tinjau pada saat kita melakukan penelitian, probabilitas memiliki beberapa
fungsi antara lain:
- Membantu peneliti dalam pengambilan keputusan yang lebih tepat.
- Dengan teori probabilitas kita dapat menarik kesimpulan secara tepat atas hipotesis yang terkait tentang karakteristik populasi.
- Mengukur derajat ketidakpastian dari analisis sampel hasil penelitian dari suatu populasi.
PENDEKATAN PROBABILITAS
Ada 3 (tiga) pendekatan konsep untuk
mendefinisikan probabilitas dan menentukan nilai-nilai probabilitas, yaitu :
- Pendekatan Klasik
Probabilitas suatu peristiwa
= Jumlah kemungkinan hasil / Jumlah total kemungkinan hasil
Jika ada a kemungkinan yang
dapat terjadi pada kejadian A dan ada b kemungkinan yang dapat terjadi pada
kejadian A, serta masing-masing kejadian mempunyai kesempatan yang sama dan
saling asing, maka probabilitas/peluang bahwa akan terjadi a adalah:
(A) = a/a+b ; dan peluang
bahwa akan terjadi b adalah: P (A) = b/a+b
Contoh:
Pelamar pekerjaan terdiri
dari 10 orang pria (A) dan 15 orang wanita (B). Jika yang diterima hanya 1,
berapa peluang bahwa ia merupakan wanita?
Jawab: P (A) = 15/10+15 = 3/5.
2. Pendekatan Relatif
Besarnya probabilitas suatu peristiwa tidak dianggap sama, tetapi tergantung
pada berapa banyak suatu peristiwa terjadi dari keseluruhan percobaan atau
kegiatan yang dilakukan. probabilitas dapat dinyatakan sebagai berikut :
Probabilitas kejadian relatif
= Jumlah peristiwa yang terjadi / Jumlah total percobaan atau kegiatan.
Jika pada data sebanyak N
terdapat a kejadian yang bersifat A, maka probabilitas/peluang akan terjadi A
untuk N data adalah: P (A) = a/N
Contoh:
Dari hasil penelitian
diketahui bahwa 5 orang karyawan akan terserang flu pada musim dingin. Apabila
lokakarya diadakan di Puncak, berapa probabilitas terjadi 1 orang sakit flu
dari 400 orang karyawan yang ikut serta?
Jawab: P (A) = 5/400 = P (A) =
1/80.
3. Pendekatan Subjektif
Besarnya suatu probabilitas didasarkan pada penilaian pribadi dan dinyatakan
dalam derajat kepercayaan. Penilaian subjektif diberikan terlalu sedikit atau
tidak ada informasi yang diperoleh dan berdasarkan keyakinan.
DISTRIBUSI PROBABILITAS
Kunci aplikasi probabilitas dalam statistik adalah memperkirakan
terjadinya peluang/probabilitas yang dihubungkan dengan terjadinya peristiwa
tersebut dalam beberapa keadaan. Jika kita mengetahui keseluruhan probabilitas
dari kemungkinan outcome yang terjadi, seluruh probabilitas kejadian tersebut
akan membentuk suatu distribusi probabilitas.
- Distribusi Binomial (Bernaulli)
Ciri-ciri distribusi
Binomial adalah sebagai berikut:
- Setiap percobaan hanya memiliki dua peristiwa, seperti ya-tidak, sukses-gagal.
- Probabilitas suatu peristiwa adalah tetap, tidak berubah untuk setiap percobaan.
- Percobaannya bersifat independen, artinya peristiwa dari suatu percobaan tidak mempengaruhi atau dipengaruhi peristiwa dalam percobaan lainnya.
- Jumlah atau banyaknya percobaan yang merupakan komponen percobaan binomial harus tertentu.
Simbol peristiwa Binomial = b
(x,n,p)
Ketarngan :
b = binomial
x = banyaknya sukses yang diinginkan (bilangan random)
n = Jumlah trial
p = peluang sukses dalam satu kali trial.
2. Distribusi Poisson
Distibusi Poisson merupakan distribusi probabilitas untuk variabel
diskrit acak yang mempunyai nilai 0,1, 2, 3 dst. Distribusi Poisson adalah
distribusi nilai-nilai bagi suatu variabel random X (X diskrit), yaitu
banyaknya hasil percobaan yang terjadi dalam suatu interval waktu tertentu atau
disuatu daerah tertentu. Fungsi distribusi probabilitas diskrit yang sangat
penting dalam beberapa aplikasi praktis.
Poisson memperhatikan bahwa distribusi binomial sangat bermanfaat dan dapat menjelaskan dengan sangat memuaskan terhadap probabilitas Binomial b(X│n.p) untuk X= 1,2,3 …n. namun demikian, untuk suatu kejadian dimana n sangat besar (lebih besar dari 50) sedangkan probabilitas sukses (p) sangat kecil seperti 0,1 atau kurang, maka nilai binomialnya sangat sulit dicari. Suatu bentuk dari distribusi ini adalah rumus pendekatan peluang Poisson untuk peluang Binomial yang dapat digunakan untuk pendekatan probabilitas Binomial dalam situasi tertentu. Contoh Distribusi Poisson:
- Disuatu gerbang tol yang dilewati ribuan mobil dalam suatu hari akan terjadi kecelakaan dari sekian banyak mobil yang lewat.
- Dikatakan bahwa kejadian seseorang akan meninggal karena shock pada waktu disuntik dengan vaksin meningitis 0,0005. Padahal, vaksinasi tersebut selalu diberikan kalau seseorang ingin pergi haji.
Percobaan Poisson
memiliki ciri-ciri berikut :
- Hasil percobaan pada suatu selang waktu dan tempat tidak tergantung dari hasil percobaan di selang waktu dan tempat yang lain terpisah.
- Peluang terjadinya suatu hasil percobaan sebanding dengan panjang selang waktu dan luas tempat percobaan terjadi. Hal ini berlaku hanya untuk selang waktu yang singkat dan luas daerah yang sempit.
- Peluang bahwa lebih dari satu hasil percobaan akan terjadi pada satu selang waktu dan luasan tempat yang sama diabaikan.
Distribusi poisson
banyak digunakan dalam hal:
- Menghitung Probabilitas terjadinya peristiwa menurut satuan waktu, ruang atau isi, luas, panjang tertentu, saeperti menghitung probabilitas dari: Kemungkinan kesalahan pemasukan data atau kemungkinan cek ditolak oleh bank. Jumlah pelanggan yang harus antri pada pelayanan rumah sakit, restaurant cepat saji atau antrian yang panjang bila ke ancol.Banyaknya bintang dalam suatu area acak di ruangangkasa atau banyaknya bakteri dalam 1 tetes atau 1 liter air. Jumlah salah cetak dalam suatu halaman ketik. Banyaknya penggunaan telepon per menit atau banyaknya mobil yang lewat selama 5 menit di suatu ruas jalan. Distribusi bakteri di permukaan beberapa rumput liar di ladang. Semua contoh ini merupakan beberapa hal yang menggambarkan tentang suatu distribusi Poisson.
- Menghitung distribusi binomial apabila nilai n besar (n ≥ 30) dan p kecil (p<0,1).
Jika kita menghitung
sejumlah benda acak dalam suatu daerah tertentu T, maka proses penghitungan ini
dilakukan sebagai berikut :
- Jumlah rata-rata benda di daerah S T adalah sebanding terhadap ukuran S, yaitu ECount(S)= λ S. Di sini melambangkan ukuran S, yaitu panjang, luas, volume, dan lain lain. Parameter λ > 0 menggambarkankan intensitas proses.
- Menghitung di daerah terpisah adalah bebas.
- Kesempatan untuk mengamati lebih dari satu benda di dalam suatu daerah kecil adalah sangat kecil, yaitu P(Count(S)2) menjadi kecil ketika ukuran menjadi kecil.
3. Distribusi Normal
Distribusi Normal adalah
salah satu distribusi teoritis dari variable random kontinu. Distribusi Normal
sering disebut distribusi Gauss.
Rumus Distribusi Normal
:
∫ (x) = -≈ < x >
≈ = 0
-≈ < μ > ≈ π = 3,14
e = 2,71828
Agar lebih praktis,
telah ada tabel kurva normal dimana tabel ini menunjukkan luas kurva normal
dari suatu nilai yang dibatasi nilai tertentu.
Ciri Khas Distribusi
Normal:
- Simetris
- Seperti lonceng
- Titik belok μ ±σ
- Luas di bawah kurva = probability = 1
Kurva Normal Umum
Untuk dapat menentukan
probabilitas di dalam kurva normal umum (untuk suatu sampel yang cukup besar,
terutama untuk gejala alam seperti berat badan dan tinggi badan), nilai yang
akan dicari ditransformasikan dulu ke nilai kurva normal standar melalui
transformasi Z (deviasi relatif).
Rumus:
- Kurva normal standar {N (μ = 0, σ = 1)}
- Kurva normal umum {N (μ,σ)}
TEOREMA
BAYES
Teorema Bayes adalah sebuah teorema dengan dua penafsiran berbeda.
Dalam penafsiran Bayes, teorema ini menyatakan seberapa jauh derajat
kepercayaan subjektif harus berubah secara rasional ketika ada petunjuk baru.
Dalam penafsiran frekuentis teorema ini menjelaskan representasi
invers probabilitas dua kejadian. Teorema ini merupakan dasar dari statistika Bayes dan memiliki penerapan dalam sains, rekayasa, ilmu ekonomi (terutama ilmu ekonomi
mikro), teori
permainan, kedokteran dan hukum. Penerapan teorema Bayes untuk memperbarui kepercayaan dinamakan
inferens Bayes.
Teorema Bayes, diambil dari nama Rev. Thomas Bayes, menggambarkan hubungan antara peluang bersyarat dari dua kejadian A dan B sebagai berikut:
P(A | B) =
|
P(B | A) P(A)
|
P(B)
|
or
P(A | B) =
|
P(B | A) P(A)
|
P(B | A)P(A) + P(B | A)P(A)
|
Misalkan kawan Anda bercerita dia bercakap-cakap akrab dengan seseorang lain di atas kereta api. Tanpa informasi tambahan, peluang dia bercakap-cakap dengan perempuan adalah 50%. Sekarang misalkan kawan Anda menyebut bahwa orang lain di atas kereta api itu berambut panjang. Dari keterangan baru ini tampaknya lebih bolehjadi kawan Anda bercakap-cakap dengan perempuan, karena orang berambut panjang biasanya wanita. Teorema Bayes dapat digunakan untuk menghitung besarnya peluang bahwa kawan Anda berbicara dengan seorang wanita, bila diketahui berapa peluang seorang wanita berambut panjang.
Misalkan:
- W adalah kejadian percakapan dilakukan dengan seorang wanita.
- L adalah kejadian percakapan dilakukan dengan seorang berambut panjang
- M adalah kejadian percakapan dilakukan dengan seorang pria
Kita dapat berasumsi bahwa wanita adalah setengah dari populasi. Artinya peluang kawan Anda berbicara dengan wanita,
Misalkan juga bahwa diketahui 75 persen wanita berambut panjang. Ini berarti bila kita mengetahui bahwa seseorang adalah wanita, peluangnya berambut panjang adalah 0,75. Kita melambangkannya sebagai:
Sebagai keterangan tambahan kita juga mengetahui bahwa peluang seorang pria berambut panjang adalah 0,3. Dengan kata lain:
Di sini kita mengasumsikan bahwa seseorang itu adalah pria atau wanita, atau P(M) = 1 - P(W) = 0,5. Dengan kata lain M adalah kejadian komplemen dari W.
Tujuan kita adalah menghitung peluang seseorang itu adalah wanita bila diketahui dia berambut panjang, atau dalam notasi yang kita gunakan, P(W|L). Menggunakan teorema Bayes, kita mendapatkan:
Di sini kita menggunakan aturan peluang total. Dengan memasukkan nilai-nilai peluang yang diketahui ke dalam rumus di atas, kita mendapatkan peluang seseorang itu wanita bila diketahui dia berambut panjang adalah 0,714. Angka ini sesuai dengan intuisi awal kita, bahwa peluang kawan kita itu bercakap-cakap dengan wanita meningkat.
Dari contoh di atas kita bisa merumuskan teorema Bayes secara umum.
Daftar Pustaka:
M.B.A,Riduan.2006.Dasar-dasar Statistik.Bandung:ALFABETA
Pratiknya.Dasar-dasar Metodologi Penelitian dan Kesehatan, Jakarta, Raja Grapindo Persada; 2000.
Https://id.wikipedia.org/wiki/Peluang_(matematika)
Https://fallawatekke.wordpress.com/2015/03/15/probabilitas-dan-statistika/
Http://www.academia.edu/11269856/STATISTIKA_-_PROBABILITAS
Https://id.wikipedia.org/wiki/Teorema_Bayes
Http://muhammadyaniishak.blogspot.co.id/2014/08/makalah-teorema-bayes.html




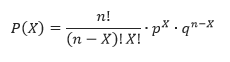

Komentar
Posting Komentar